The Developer’s Cry

 a blog about computer programming

Fun With Fixed Point

While I was programming a retro platformer, I naturally made use of 32-bits floating point math to implement the jump physics (which is kind of an interesting topic in itself). It gave a funny feeling, because the hardware of the 1980s was not equipped for floating point. How did they do it then? There were early jumping games (Donkey Kong, Manic Miner), but Super Mario Bros. from 1985 has a perfectly calculated jump, and others soon followed. Oh, and let’s not forget space sim Elite (1984) featuring 3D vector graphics on an 8-bit micro computer. Rather than floating point, the calculations used fixed point.

Fixed point is a scheme in which the decimal point of a number is at a fixed position; either you have n decimal digits after the comma, or you can have a fixed n binary digits representing the fraction.

A game of numbers

An easy way of explaining fixed point is with money: if the price of a soda is 2.95 eurodollars, then we can store that in computer memory as 295 cents. Another good example is distances: 1 meter is 100 centimeters. No floats needed if you scale everything by a smaller unit.

Likewise, if we reserve 8 bits for the fraction, then our scaling factor is 256. This gives us a precision of well over 2 decimals after the comma.

“But that’s imprecise!”, I hear you say.

What is precision? Floating point is imprecise by its very nature. Put an arbitrary large number in Excel and calculate + 1, and be amazed at how it can’t be done—you get a wrong result because floating point can’t represent the exact value. Proof:

// 100 GB as float
float f = 100000000000.0f;
printf("%f\n", f);

This prints the number 99999997952.000000. The difference is 2048, which seems pretty far off. The compiler doesn’t even give a warning. Even weirder, adding 1.0f results in the same 99999997952.000000 (!) because float lacks precision. Computers work with a limited set of bits and can’t magically represent every imaginable value.

In a strange way, fixed point can be more precise than floating point. Imagine modeling the universe in 64-bits integer + 64-bits fraction.

A fixed point representation using only 8 bits can not make steps smaller than 1/256 = 0.00390625, but for putting pixels on a screen in a retro game, that’s pretty damn precise.

[Note that 7 bits suffices for having two decimals after the comma. Going with 8 bits was more attractive somehow, and is twice as precise].

Conversion and arithmetics

Those poor souls clever coders in the 1980s had to juggle two words for storing the integer and fraction. We are lucky to have 64 bits wide integers on a modern computer. For my retro game I use 32-bits ints; 24 bits for the integer part, and 8 bits for the fractional part.

This gives us a range of -8388608.0 to 8388608.0 (that is 8 × 1024 × 1024).

typedef int32_t fxp;

// scaling factor represents value 1.0
#define FXP_ONE        ((fxp)(1 << 8))

fxp fxp_from_float(float f) {
    // Converts float to fixed point type
    return (fxp)(f * FXP_ONE);
}

float fxp_to_float(fxp p) {
    // Converts fxp back to type float
    return (float)p / FXP_ONE;
}

Addition and subtraction just work the same as always. Comparisons just work. Negative numbers work, and you can test the sign bit for negativity. The fxp_abs(x) function is trivial to write.

(Don’t) panic!

For multiplication and division we have to do something special. When you multiply meters by meters, the result has unit meters-squared. This means our result is going to be off by a factor of scale, and thus we must scale back to meters; divide by the scaling factor.

On top of that, when doing this calculation the intermediate value may become so large that we don’t have enough bits to store it. A larger integer type is required for storing the intermediate. We can cheat a little; nowadays we have the luxury of a 64-bits system, so let’s take advantage of that.

fxp fxp_mul(fxp a, fxp b) {
    int64_t m = ((int64_t)a * (int64_t)b) / FXP_ONE;
    return (fxp)m;
}

fxp fxp_div(fxp a, fxp b) {
    int64_t d = ((int64_t)a * FXP_ONE) / (int64_t)b;
    return (fxp)d;
}

WAIT!! What about division by zero? There is nothing special about it, really. Div by zero acts in same the way it always does; the system will fault and generate an exception. There is no need to take special action from the point of view of a fixed point number library.

It may get a little tedious having to write fxp_mul() and fxp_div() but that’s just how it is. In C++ you can enjoy operator overloading and fxp will feel like a natural numerical type.

The modulo can be computed as:

fxp_mod(a, b) => a - b * floor(a / b)

The fxp_floor(x) function simply clears the 8 bits that make up the fraction.

Rounding up is simply adding one half and floor-ing (truncating) the result. Negative numbers round down, so subtract one half instead.

Less trivial to implement are square root and trigonometry functions. Now we get into the field of numerical analysis, where we use algorithms to compute approximate values.

The square root of all evil

Square root can be calculated via Newton-Rhapson method. It is an iterative method in which the computed value converges to the correct answer. A sloppily coded version will easily slip into an endless loop.

/*
    you can tweak the precision
    we desire to be as precise as possible
*/
const fxp precision = (fxp)0;

fxp x_n;
fxp x = a;
while (fxp_abs(a - fxp_mul(x, x)) > precision) {
    x_n = x;
    x = fxp_div(x + fxp_div(a, x), 2 * FXP_ONE);
    if (x == x_n) {
        break;
    }
}

The square root of zero is zero, but floats may actually be minus zero, in which case the C math function sqrt() returns minus zero. Mind you, in math there is no such thing as “minus zero”. Nor can we represent such thing in fxp.

The square root of a negative number is undefined. The C function sqrt() returns NaN and sets errno to EDOM (domain error). We don’t have any special bit for specifying NaN though—we could let FXP_MIN double as FXP_NAN. This would work because sqrt can not return a negative value anyway.

The introduction of NaN however opens a new can of worms … because no further computations may take place when a NaN enters the field. Having a special value take the form of NaN is cumbersome, so much so that since this is my personal library anyway, I let fxp_sqrt(x) panic for negative x. Crashing is very definitive, but I refuse having to deal with NaN in game code.

Surfing the waves

The sine of an angle (in radians) is approximated by a Taylor series polynomial:

sin(x) => x - x**3/3! + x**5/5! - x**7/7! + x**9/9! - ...

where x is between -pi and pi radians
and x**N is x to the power N
and N! is N factorial

In principle the series continues with repeating terms ad infinitum. Writings on the internets say that the 7th degree is “good enough”, but actually the 9th degree term is where we reach the limits of 8-bits precision. The function is very accurate, it delivers production grade sin().

Don’t forget to convert pi into a fixed point number, too;

fxp p_pi = fxp_from_float(M_PI);

// or just use a constant:
// PI = fxp_from_float(3.14159 ...)
#define FXP_PI      ((fxp)0x324)

The cosine is another Taylor series:

cos(x) => 1 - x**2/2! + x**4/4! - x**6/8! + x**8/8! - ...

where x is between -pi and pi radians

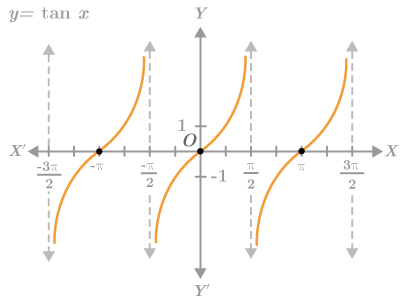
Tangential issues

Next up is the tangent. While tangent seems boring (I don’t use it much in practice) it is maybe the most interesting of all. It is approximated by a Maclaurin series:

tan(x) => x + x**3/3 + 2x**5/15 + 17x**7/315 + 62x**9/2835
    + 1382x**11/155925 + ...

where x is between -pi/2 and pi/2 radians

This series proves to be challenging for fxp as well as float. You need many terms to make it accurate close to pi/2, but especially fxp lacks the precision to calculate more terms. It simply can’t do it.

No worries though, remember from school that the tangent equals sine div cosine.

tan(x) => sin(x) / cos(x)

where x could be between -pi and pi radians, but ...

Mind that cosine pi/2 equals zero, which means we divide by zero. Mathematically this is correct, the tangent function has a discontinuity at pi/2; values close to pi/2 approach infinity, but for pi/2 itself the function is undefined. It does not compute.

Then why is it that tan(pi/2) in the C math library returns a value? Adding insult to injury, tanf(pi/2) (for float rather than double) returns a negative value, which is completely wrong! Even Python, which originated at a mathematical centre and is usually quite pedantic about these things, does not raise an exception.

C using float:
tanf(M_PI * 0.5f) == -22877332.000000

C using double:
tan(M_PI * 0.5) == 16331239353195370.000000

Python:
math.tan(math.pi / 2) == 1.633123935319537e+16

We really ought to be triggering a fault, or else get a NaN, right? This is nuts and leads to all sorts of wild speculation from my side. Is it because internally they use a Maclaurin series? Is it due to imprecision? Or is the issue at a more fundamental level? I mean, even 64 bits can not hold the exact value of pi, because the number of digits in pi is infinite. Even worse, 0.0f is not exactly the same as mathematical zero? Or is it that tan() has been rigged deliberately, by design, by committee, so that it never accidentally crashes on div by zero.

Ironically enough, fxp is imprecise enough to simply fall into division by zero—which is, by all accounts, perfectly correct math. But in a world where it is generally accepted that tan(pi/2) does not crash, but returns some value, we have little choice but to rig fxp_tan(FXP_HALF_PI) accordingly and have it return FXP_MAX (!)

fxp fxp_tan(fxp a) {
    fxp sin_a = fxp_sin(a);
    fxp cos_a = fxp_cos(a);
    if (cos_a == (fxp)0) {
        /*
        hack the planet: tan(PI/2) is undefined
        and should really FPE with div by zero

        But the world seems to have generally
        accepted that in computer software
        tan(PI/2) returns a value
        */
        if (sin_a < 0) {
            return FXP_MIN;
        }
        return FXP_MAX;
    }
    return fxp_div(sin_a, cos_a);
}

So there you have it. It’s not good math, but I guess it passes for computer science.

Rounding up

Contrary to popular belief, math does not always translate well to computers. Number systems and computation in software are riddled with peculiarities, highlighting that even modern computers have their limits. That aside, fixed point works like a charm. The perceived lack of precision is mostly an illusion, and in fact fixed point can be very precise for the domain it operates in. For example, when doing jump physics in a 2D retro game.