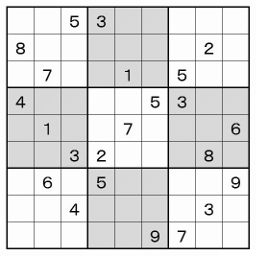
Solving the mother of all sudoku puzzles
 This post is all about sudoku, the venerable Japanese puzzle. Even though
the hype lies far behind us, every once in a while I get bored and return to
solving a few puzzles. But then one day I was given an exceptionally hard
to beat sudoku puzzle. Even after hours of staring it down, I wasn’t getting
anywhere. Hmmm… I was not going to be belittled by some stupid puzzle!
And so I decided to cheat a little and crack it by writing a sudoku solver.
This post is all about sudoku, the venerable Japanese puzzle. Even though
the hype lies far behind us, every once in a while I get bored and return to
solving a few puzzles. But then one day I was given an exceptionally hard
to beat sudoku puzzle. Even after hours of staring it down, I wasn’t getting
anywhere. Hmmm… I was not going to be belittled by some stupid puzzle!
And so I decided to cheat a little and crack it by writing a sudoku solver.
Sudoku is a numbers game, but there is no calculation involved whatsoever.
The ‘game board’ is a set of 9×9 tiles, each containing a number from
1 to 9. The numbers in a row must be unique, however, as well as the numbers
in each column, and the numbers in each 3×3 sub block.
Some numbers are given; it is up to you (the player) to fill in the gaps.
Once all the numbers are filled in according to the given rules, the puzzle
is solved. In general, a sudoku puzzle has one, and only one, unique solution.
First of all, let me mention that brute-forcing it is a definitive no-no.
There are countless possibilities that do not lead to the solution. I figured
that the total number of permutations would be around 9×9! (over 3 million),
but two researchers have calculated that there are 5,472,730,538 (almost
5.5 billion) essentially different sudoku grids. The number of raw
permutations is much larger however, in the range 6.67×1021.
Trying them all is going to take forever, even on the fastest computer
available today. We need to be smarter than that—why not simply play the
game and see where it gets us?
In order to let the computer play, we are going to need a couple of routines:
- load a given sudoku puzzle
- check whether puzzle is correct
- find cell with only one possibility left
It’s easy enough to store the puzzle into a 9×9 array of cells. Each
cell holds a number, but also has a property saying whether it’s a ‘solid’
cell, or can be filled in by the player.
Checking the correctness of the puzzle is a three-step process: check all
the rows, columns, and 3×3 blocks. Finding a cell with only one possibile
solution also checks all the rows, columns, and 3×3 blocks.
This is a reasonable start for a solver program, but note that it will only solve the most naive beginner-level sudoku puzzles. The problem is, there will be cells that have more than just one option, and this solver is just not good enough. For the super evil sudoku, we are going to have to do better than this.
Rather than finding a cell with only one possible solution left, let’s take a look at what possible solutions there are for a blank cell. A blank cell may have any number between 1 and 9, unless that number is already present in that row, column, or 3×3 block. Any already filled-in numbers are removed from the set of possible solutions for the cell. The remaining set holds a number of possiblities, of which one is the solution for this cell. Let’s try them all, but because we want to have the solution as quickly as possible, start with the cell that has the smallest set. So if there is a cell with only one or two possible solutions, try that one first before moving on to harder to crack cells.
As you are trying out possible solutions, the numbers lock into place and they can no longer be part of solution sets in other cells that are in the same row, column or block. Slowly, the puzzle is being solved. But we may still hit a wall and have to go back to the point where we tried a wrong possibilty; this happens because not all attempts lead to a perfect puzzle. Many configurations are invalid, and need to be discarded.
Going back is easily done by means of backtracking. Backtracking works by
recursion. I find it easy to think about in terms of functional programming;
in functional programming, objects are immutable, they can not be changed.
If you wish to change the state of an object, then that is a new object,
albeit a modified clone of the object.
So whenever trying a solution to a cell, clone the whole puzzle. Put that
puzzle object onto a stack. Now recurse, and try solving the next cell.
If the puzzle is invalid, backtrack: pop the stack and return. As the recursive
function is returning, it will continue trying the next solution to the
cell. Notice how cells that ‘work’ are followed-up on and lead to the next
step in solving the puzzle, and solutions that don’t work tend to cut off
excess work.
I implemented this solver in Python. Detail: cloning is done with
copy.deepcopy(). My aging computer solves the evil sudoku in under half a
second. On the Raspberry Pi 2 it takes 3.5 seconds. Remember that
brute-forcing would take forever. You don’t need a fast computer (nor a
low-level programming language) to pull this off. What’s important is choosing
the right algorithm.
Backtracking is the algorithm for this kind of puzzles, where a partial list of candidates could lead to a solution. In fact, after finding a solution, the algorithm may continue to run and find all solutions. In a bold move, I handed it a completely blank 9×9 grid. It started spewing out all solutions to sudoku … each and every sudoku there is, ever was, or ever will be. And after a while, I hit Ctrl-C.