Sunday, May 21, 2017

Last time I wrote about quaternions. What again are quaternions? In short, they are rotations in complex space. Quaternions can relatively easily do a neat trick that is difficult to do using Euler angles: rotate from one arbitrary orientation to another with constant angular velocity, or in other words, perform spherical linear interpolation.

With SLERP you might smoothly rotate an object, but where it really shines is for a rotating camera. The key point to keep in mind here is ‘constant angular velocity’, meaning it will rotate steadily and without any side effects like hiccups or sudden turns.

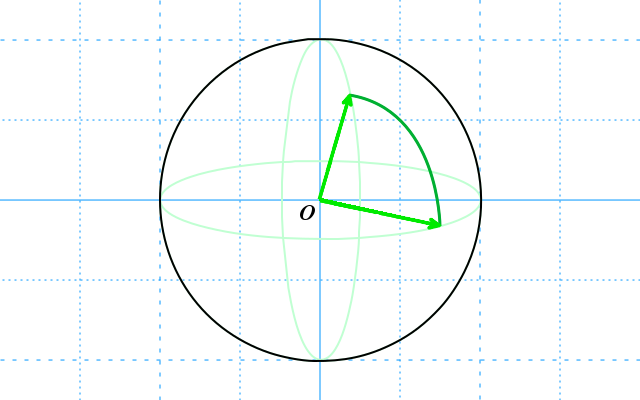
An image helps to visualize what we’re trying to do:

Suppose the vectors were described using Euler angles, the first trouble is that rotations are not commutative; the outcome depends on the order in which you apply each X, Y, Z rotation. You can work around this by defining a fixed order, but you are not going to get good slerping results if you rotate in more than one dimension at a time. Now let’s say that the portrayed vectors are quaternions in the 4D unit sphere. We can now describe the path between the two points. Each point on on that path is again given by a quaternion; a rotation that lies in between the starting and end orientation.

Let’s first have a look at linear interpolation between to values, from a to b. The parameter t is a floating point value between 0 and 1.

float lerp(float a, float b, float t) {
    assert(t >= 0.0f && t <= 1.0f);
    return (1.0f - t) * a + t * b;
}

That’s simple enough. Why use (1.0f - t)? That is to guarantee that we get precisely b when t == 1.

Now on to the slerp routine. We wish to interpolate from a quaternion to another quaternion, again with parameter t between 0 and 1. The output will be a new quaternion that represents the interpolated orientation.

quat quat::slerp(const quat& to, float t) const {
    quat qb = to;

    // cos(a) = dot product
    float cos_a = x * qb.x + y * qb.y + z * qb.z + w * qb.w;
    if (cos_a < 0.0f) {
        cos_a = -cos_a;
        qb = -qb;
    }

    // close to zero, cos(a) ~= 1
    // do linear interpolation
    if (cos_a > 0.999f) {
        return quat(lerp(x, qb.x, t), lerp(y, qb.y, t),
            lerp(z, qb.z, t), lerp(w, qb.w, t));
    }

    float alpha = acosf(cos_a);
    return (quat(*this) * sinf(1.0f - t) + qb * sinf(t * alpha)) / sinf(alpha);
}

It’s probably a bit difficult to grasp just what is going on here. If you look at the drawing of the unit sphere, you will notice that the two vectors appear to lie in a 2D plane, sliced from a 3D sphere. This means we can use spherical interpolation of vectors; we can calculate any point on the path with trigonometry. When you work out the math, you get a formula exactly like the final line of code with lots of sines in it.

For that formula we need to know the angle between the two vectors. The cosine of the angle between two vectors is given by the dot product. This is a mathematical property of vectors. If the dot product is negative, it’s a reflex angle. For quaternions this means that it’s taking the long path around the sphere. To take the shortest path, simply negate the quaternion to make it take the shortest path.

Finally, the formula divides by sin(alpha), resulting in a div by zero error when the angle is zero. To prevent this from happening, resort to linear interpolation when the angle gets close to zero—ie. the cosine gets close to one.

Next is a simple example of how to use the slerp routine. Here we rotate a model back and forth:

quat qa(120, 0, 1, 0);  // turned away from view
quat qb(45, 0, 0, 1);   // roll on side

constexpr float step = 0.01f;
static float t = 0.0f;
static bool direction = true;

if (direction) {
    t += step;
} else {
    t -= step;
}
if (t <= 0.0f || t >= 1.0f) {
    direction = !direction;
}

quat qc = qa.slerp(qb, t);

mat4 model = qc.matrix();
load_matrix(model);

Note that we convert the resulting quaternion back to a matrix for use with OpenGL. Here we load the model matrix. Of course you might do this with the view matrix instead to create a smoothly rotating camera.

That’s all folks. Happy slerping!