Sunday, November 27, 2022

An important topic in gamedev is collision detection. For a classic 2D arcade game we can suffice with a simple overlapping rectangle test: if the player rect intersects with the monster rect, then it’s a hit (and we’re dead). The overlapping rectangle test is trivial to implement, but it is also a crude test, resulting in false positives and frustrated players. The test is crude because the bounding rect does not trace the shape of the (player) sprite very accurately. One fix is to use multiple hitboxes to try approximate the shape of the collider more closely. The more common way is to use circles and capsules as collision shapes, as well as rectangles. These shapes can all collide, and a convenient way of detecting intersection is by using the Minkowski sum.

Minkowski sum

The Minkowski sum of two shapes is a mathematical definition that adds up two shapes. Adding up two shapes together may sound a bit strange, but consider that a rectangle’s space can be expressed by an x- and a y-vector, then you can add up two of these vectors, and the result will be larger vectors, describing a large rectangle.

When we add up a rectangle and a circle, the result is a rounded rect.

Collision detection

Two shapes collide when they intersect. For two circles it’s easy to understand that they intersect when the center point of the colliding shape is inside the enclosing circle that is the sum of the two radii; in other words, when the center point is in the Minkowski sum of the two circles. The same holds true for other shapes: we can collide a square with a capsule shape, and if the center point is inside their Minkowski sum then it’s a hit.

This will work for any convex shape; in principle you can now reliably collide hexagons with pentagons, for example.

Essential ingredients for collision testing a shape:

• it must be a convex shape
• what is its center point
• the shape itself must be defined relative to its center point. (See what that means for an AABB with origin at bottom-left corner..?)
• a .contains_point() method that determines whether a given point is inside or outside the shape

The difference is in the difference

To make the code work we actually need the Minkowski difference:

M = A + (-B)

That minus sign makes a big difference.

Any written text on the internets about this subject largely refer to “Minkowski sum” and end up using Minkowski difference. I have accepted this as ‘gamedev jargon’ and let go of the slip in mathematical correctness.

Implementation

We can write this in code by implementing the shapes Rect, Circle, RoundedRect. There are two kinds of axis-aligned capsules: vertical and horizontal Capsules.

The pseudo code is very simple:

func collision(a: Shape, b: Shape) -> bool {
    //
    // shapes a and b collide if their center point
    // is inside the minkowski sum shape
    //
    let m: Shape = minkowski_sum(a, b)
    let p: Point = b.center()
    return m.contains_point(p)
}

In Rust, all permutations of colliding shapes are implemented as separate functions for each specific case. In C++, you can try the object-oriented solution (such as using a CollisionShape base class), and that didn’t work well for me, in the sense that it doesn’t give any advantage or result in cleaner code. You still have to write out all the code for colliding a shape A with a different shape B.

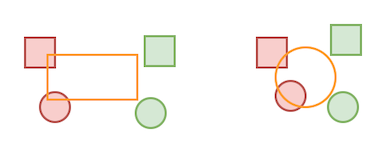
All in all, it’s a bunch of work (!) and you have to be precise not to introduce any bugs. You can (and should) visually debug it by rendering the collision shapes.

The image shown is a mockup of the result, showing the intersecting shapes in red.

Note that you can have oddly shaped objects (e.g. diamonds), as long as they are convex, and implement the center() and contains_point() methods. You are not limited to rectangles and circles alone.

Remarks

You should also do a fast pre-collision test, such as using a collision grid or a bounding rect or bounding circle test.

This method works for shapes rotated under an angle, if you go through the trouble of treating them as -and calculating- individual triangles of a mesh.

This method is also valid for 3D, where you would typically test against spheres, cylinders, and 3D capsules.

Pro game programmer Casey Muratori talks at length about Minkowski sum on YouTube. Look him up if you have a couple of hours to spend.