The Developer’s Cry

 a blog about computer programming

LeetCode Is Leet

There is a “leetcode challenge” on the net that reads: implement is-sudoku-valid in assembly language. I watched Primeagen mess around live on-stream, and being a bit of a sudoku-nut myself, I figured I would take a stab at it, too. My personal spin: using arm64 assembly. And so I saved a raspberry pi 4 from a drawer and booted up.

The raspberry pi 4 is a neat little computer that is capable of running a 64-bit operating system. It’s not the fastest system, and its I/O is particularly slow, but the neat part is, we get to code in arm64 assembly for Linux. We need to get a few things straigthened out before we can actually dive into the code.

ARM64 code is different from ARM32 code. Any examples on the internets mentioning “register R0” are no good; aarch64 is a different architecture, and therefore also has a different assembly language. It also comes with its own conventions that we should adhere to.

For the unwary, the above means that any subroutine may clobber registers x0-x15 at any time. If you need to preserve their values, use x19-x28 instead. A subroutine that needs to use x19-x28 for something else, should save the register on the stack and restore it before returning. Registers x16, x17 may be used across subroutines, but you should take care that they stay valid and correct for all code paths.

You may wonder why there is no register x31. The instruction encoding uses number 31 for either the stack pointer or the special zero register xzr, a read-only register that always reads zero. Just another ARM trick: copying (zero) from a register is much faster than loading a zero value from memory.

The x-registers are 64 bits wide. Use w0-w30 to address the lower 32 bits of the register. Doing so automatically zero-extends the upper 32 bits of the register. There are instructions that deal with loading and storing individual bytes, but on ARM you can’t address the lower byte of a register like you would on x86.

Eight arms to hold you

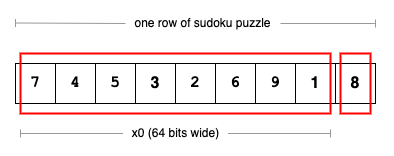
For the sudoku challenge we will be loading bytes (sudoku digits) into 64-bits wide registers. A sudoku row has nine numbers. For checking the validity of a row, we can load 8 bytes at once (64 bits), and then load the remaining byte.

    /* x1 := address of sudoku puzzle, first row */
    ldr x1, =sudoku

    /*
        load 8 digits into x0
        afterwards x1 points at digit 9
    */
    ldr x0, [x1], #8


    /* ... and later on ... */

    /*
        load 9th digit into x0
    */
    ldrb w0, [x1], #1

A row is valid when all digits 1 to 9 are present, each used exactly once. What we can do is keep a table, or … we can set a bit for each digit that is present. If all digits are present, then we should end up with having nine bits set.

So, we have 8 digits in x0. We want to take one digit (one byte) from it, and then set a bit for it in another register—I’ll pick x6 for this (because, why not).

We can calculate the bit number by shifting the value 1 to the left. In pseudo-code:

        nine_bits = 0
        digit = (byte)(x0 & 0xff)
        bit = (1 << digit)
        nine_bits |= bit

This can easily be translated to assembly language. The only thing is, in assembly language you can’t have an immediate value at the lefthand side of a shift operation. So we use a register (x4) to hold the value 1.

    /* nine_bits are clear */
    mov x6, xzr

    /* x2 := digit = (byte)(x0 & 0xff) */
    and x2, x0, #0xff

    /* x2 := bit = (1 << digit) */
    mov x4, #1
    lsl x2, x4, x2

    /* x6 := nine_bits |= bit */
    orr x6, x6, x2

Now loop eight times to gather all bits. To get the next digit from x0, we must “shift out” the byte we just processed.

    /* x0 := x0 >> 8 */
    lsr x0, x0, #8

After looping eight times (not shown here) we have processed eight numbers of the sudoku puzzle. The nineth number in the row is added as a separate step. Next, we check whether x6 has all nine bits set.

But wait, what happens if the row contains the number 7 twice? Then bit #7 will be (doubly) set, but some other bit will be missing. The only way the row can be correct, is to end up with nine bits set.

Also, mind that sudoku uses numbers 1 to 9, and therefore bit zero remains unset.

    /*
        if not all nine bits set,
        then it's an invalid row
    */
    cmp x6, 0b01111111110
    bne invalid_row

If we fell through, the row is valid! Loop nine times to check all rows (not shown here).

A little bit more

Above we are loading eight numbers at a time into a register. The sudoku row is 9 numbers long, so we fell one short. It is possible to encode a digit in just 4 bits (a nibble) … making it possible to fit 16 digits into a single register. So we can make it load an entire row at once, if we really want to.

Encoding the sudoku in nibbles does not make life easier for checking the rest of the puzzle though, so I will leave it at that.

However! There is another clever trick that we can do. Checking columns makes us jump through memory, and checking blocks is a tedious bit of code. But what we can do is change the memory layout of columns and blocks; they are again a group of nine numbers, if we transpose them to a horizontal layout in memory, then we can use the same subroutine for checking rows, columns, and blocks. (Bonus points, I guess).

Sudoku make me a sandwich

Checking a sudoku puzzle for validity is not a super difficult programming problem. The key is to break the problem down into smaller parts, and this is especially true for programming in assembly language.

A sudoku puzzle is solved when:

So, in code (be it assembly or not) these three rules can be written as:

check_rows
check_columns
check_blocks

Now, let’s break it down further:

check_rows:
    check_row i
    loop 9 times

check_columns:
    check_column j
    loop 9 times

check_blocks:
    check_block k
    loop 9 times

Keep breaking it down, and the assembly code basically writes itself. So much so, I wrote multiple implementations. Find the full codes on github.