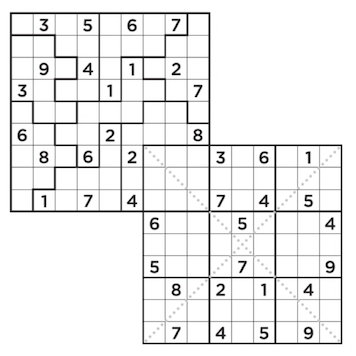
Sudoku Mix
After the glorious victory over the sudoku triathlon puzzle in the previous
post, there was nothing left to do but move on to the next sudoku challenge.
My sister was so kind to mail me a picture of a “sudoku mix” puzzle,
taken from a local newspaper. This particular puzzle is a combination
of a jigsaw sudoku and a diagonal sudoku.
The puzzle is a two-headed monster. How does one slay such an abomination?
Obviously it consists of two sudoku puzzles. While it is kind of possible
to solve both parts independently, the puzzle must be solved as a whole
to find the one true solution. Therefore we define a single 15×15 puzzle
grid and layer on top two SudokuView instances, using the same strategy
as we did when solving the sudoku triathlon puzzle.
// Returns true if puzzle is solved
// ie. when there are no empty cells left
fn is_solved(&self) -> bool
// Returns true if puzzle is valid
// meaning each row|column|block|shape|diagonal contains
// value 1..9 exactly only once, or empty cell (zero)
fn is_valid(&self) -> bool
The mix puzzle is valid when both views are valid. Each view is a different type of sudoku, and each view has its own rules of what it means to be ‘valid’. A jigsaw sudoku is valid when each row, column, and shape contain the numbers 1 to 9. A diagonal sudoku is valid when each row, column, block, and diagonals contain the numbers 1 to 9.
#[derive(Clone, Copy, Debug)]
enum SudokuType {
Jigsaw,
Diagonal,
}
// SudokuView are only offsets;
// a 9x9 view into the SudokuMix.cells
#[derive(Clone, Copy, Debug)]
struct SudokuView {
x_offset: usize,
y_offset: usize,
puzzle_type: SudokuType,
}
For the jigsaw sudoku we need to define the jigsaw shapes. While it seems
logical to bind the shapes to the view (and you certainly can), in my
implementation the shapes are part of the entire puzzle, and the view
is kept as simple as possible. A shape is a collection of 9 cells that belong
together, and there are 9 shapes in a jigsaw sudoku. Rather than introducing
a “Shape” type, we simply use a Vec to map coordinates:
shapes_xy: Vec<Vec<(usize, usize)>>
// Returns shape index for given cell at (x,y)
fn shape_at(&self, x: usize, y: usize) -> usize
// Returns shape coordinates of a given shape
fn shape_coordinates(&self, shape_idx: usize) -> &Vec<(usize, usize)>
So, shapes are numbered 1 to 9 (or zero to eight), and thus we can easily obtain the coordinates that define the jigsaw piece. Using that, we can check whether a shape is a valid; containing only numbers 1 to 9. On top of that, we can create and maintain the solution sets for the cells of the jigsaw sudoku.
The solver for the sudoku mix puzzle works largely the same as for the triathlon puzzle in our previous post. The solver creates solution sets for each cell in the puzzle. It solves by simply trying out each potential solution, and backtracking if it doesn’t work. If a solution to a cell does work, then that number can not appear in other solution sets for that row, column, block, diagonal or jigsaw piece.
// number n is a good fit for cell (x,y)
let view = self.puzzle.get_view_xy(x, y);
let vx = x - view.x_offset;
let vy = y - view.y_offset;
self.ruleout_row(vx, vy, &view, n);
self.ruleout_column(vx, vy, &view, n);
match view.puzzle_type {
SudokuType::Jigsaw => {
// implementation detail:
// we don't use a view here
// shapes are bound to the puzzle
self.ruleout_shape(x, y, n);
}
SudokuType::Diagonal => {
self.ruleout_block(vx, vy, &view, n);
self.ruleout_diagonal(vx, vy, &view, n);
}
}
Keen observation: Ruling out the diagonals prunes away some dead branches, but the solver will still work without it. In addition to that, a regular sudoku can be seen as a special case of jigsaw sudoku where all shapes are 3×3 squares. Therefore the solver can be coded without making any distinction between jigsaw and diagonal sudoku—it wouldn’t be better code though, in my opinion.
After a bunch of debugging it managed to crack the puzzle in under one second.
Well, that was fun. Now I crave some nachos. I wonder why.